Causal Inference from Observational Data, или как провести А/В-тест без А/В-теста.
Uplift modeling, potential outcomes, CATE/LATE и вот это вот все.
Содержание:
· Введение
· Связь с ML
· Кейсы
· Терминология и предположения А/В
· Controlling for covariates в А/В-тесте
· Controlling for covariates в observational studies
· Confounders
· Matching Methods
· Propensity Score
· Doubly-robust
· Instrumental variables (IV)
· Time-series
· Regression Discontinuity Design (RDD)
· Diff-in-Diff (DiD)
· Synthetic-control (SC)
· Continuous treatment, Double machine learning
Введение
Привет дата-ниндзя👋! Первый вопрос, который ты задашь — зачем вообще это нужно ❗️❓
Предположим, ты исследуешь причинно-следственную связь между двумя величинами (Y зависит от X). И тогда, изменяя X, мы можем быть уверены что изменяем Y, причем уверены мы не только в самом факте изменения, но и в его направлении и величине (magnitude).
Конечно можно применить наивный подход — посчитать корреляцию между X и Y, но всем нам с детства твердят — Correlation does not imply causation. Нужны более строгие математические методы.
Можно привести много примеров подобных задач в дата-аналитике, вот некоторые из них:
- Анализ эффективности маркетинговых акций. Мы хотим понять, насколько увеличение числа новых регистраций объясняется запуском наружной или ТВ-рекламы (а не вызвано каким-либо внешним событием). Для подобных задач есть специальные термины— Program evaluation и Uplift Modeling.
- Создание прокси-метрик для А/В. Очевидно, что мы хотим растить долгосрочные метрики (пресловутый LTV), но проводить эксперименты длиной в год или больше — не самая лучшая затея. В таком случае мы можем ориентироваться на прокси-метрики, которые можно изменять/измерять за короткий период, и с их помощью предсказывать долгосрочные. Проблема в том, что если между выбранными short-term и long-term метриками не причинно-следственная связь, а корреляция, то изменение в short-term метрике может просто не повлиять на long-term метрику, а иногда и вовсе покрасить ее в другую сторону.
На самом деле это 2 разные задачи — поиск зависимости и оценка эффекта там, где зависимость уже есть (точнее предполагается, что есть). Эти задачи имеют общеизвестные термины — Causal Discovery и Causal Inference. Для их решения существуют 2 фреймворка — structural causal model (SCM) и potential outcome (PO). В этой статье мы разберем PO и основанные на нем методы, во второй статье поговорим про SCM и поиск зависимостей, а в третьей части используем ML и поговорим про метрики и про применение данных методологий не вместо A/B, а с ними. В целом, сейчас это модная тема (у Netflix для этого есть отдельная команда, а Booking рассказывал об этом 3 месяца назад на Web Conference), думаю, что в ближайшее время она перехайпует популярные сейчас А/В-тесты.
Связь с ML
Аналогично корреляции, применение любых ml-методов для предсказания Y c помощью X и набора других переменных также не подходит для решения перечисленных задач, поскольку показывают лишь ассоциацию, но не причинно-следственную связь.
Кроме тогда, любая интервенция (воздействие, treatment) изменяет среду (параметры модели), и ml-модель может перестать работать в новой среде. Кстати, А/В тоже подвержены этой проблеме, и ее решают с помощью т.н. switch-back дизайна (Doordash, Lyft раз и два, общая теория по этому дизайну еще в разработке).
Кейсы
Несомненно, золотым стандартом для статистического вывода результатов воздействия (treatment effect) и доказательства причинно-следственной связи являются Randomized Controlled Trials (они же A/B- или сплит-тесты, они же эксперименты) 👬. RCT находятся почти на вершине Pyramid of Evidence — уровней доказательств чего-либо (выше разве что мета-анализ).
Однако бывают кейсы, когда запуск А/В затруднен или вовсе невозможен. Несколько примеров:
- Требуется оценить эффект от фичи, которая уже работает длительное время. Конечно, можно отключить фичу для таргетной группы (ухудшающий эксперимент), но это сделает неконсистентным пользовательский опыт и повлечет большую нагрузку на команду поддержки пользователей. Недавний пример из моей работы — необходимо оценить эффект на вовлеченность пользователей и деньги от первых запущенных курсов на образовательной платформе. Ребята из Coursera также сталкивались с похожими задачами и выпустили серию статей о методах такого анализа (раз, два, три, четыре), все они будут рассмотрены в этой статье. Также иногда фича новая и только запускается, но сразу на весь трафик по велению продакт-менеджера (признайтесь, все аналитики сталкивались с такой ситуацией).
- Иногда невозможно провести эксперимент по этическим причинам — например упомянутые выше ухудшающие эксперименты на образовательной платформе заведомо (ex ante) снизят качество образования для части пользователей. Другой пример — социальные или медицинские эксперименты с высоким риском для таргетной группы.
- Ситуации, в которых не выполнены некоторые из предположений/требований для А/В-тестов. Давай их обсудим в следующем разделе.
В подобных кейсах надо оценивать эффект с помощью т.н. обсервационных исследований, когда исследователь лишь наблюдает за естественным выбором воздействия или использования той или иной фичи, а не контролирует этот процесс и не производит интервенцию.
Терминология и предположения А/В
Итак, методология А/В-тестирования основывается на Rubin causal model. Если ты давно занимаешь A/B и хорошо в них разбираешься, переходя на 2 раздела ниже. Коротко суть модели:
- существуют юниты i=1..N — клиенты, пациенты и тд;
- они находятся под определенным treatment’ом t=[0,1] — переменная, имеющая 2 разных варианта;
- потенциальные исходы (potential outcomes, также называемыми Counterfactuals) — результат или итог, верный под определенным условием (treatment’ом). Обозначается как Y(i). Как правило, это наша целевая метрика, которую мы анализируем в А/В.
- concomitants или covariates z_i — другие переменные (массив переменных), относящиеся к юниту i и влияющие на потенциальные исходы этого юнита. Например, в случае пользователя сайта, это может быть его возраст, дата регистрации или первой покупки.
Для примера: юниты — это пользователи (i) сайта онлайн-магазина, treatment (0 или 1)— это 2 различные версии платежной страницы на данном сайте, а potential outcome — конверсия в покупку данного пользователя, в зависимости от версии платежной страницы ( Y(i|t=0) и Y(i|t=1) ). На самом деле, мы должны учитывать все переменные, поэтому potential outcomes честно выражается как Y(i|t, z_i). Однако, в отличие от treatment’а, данный вектор для конкретного юнита является константой. Учитывая это, а также тот факт что все concomitants учесть нельзя (про часть мы даже не знаем), обычно пишут просто Y(i|t), но мы еще вернемся к этому. Данный набор определений и есть фреймворк Potential Outcome.
Итак, основная задача, которую решает Causal Inference и А/В-тесты в частности — определить, влияет ли treatment на potential outcome (и если влияет, то в какую сторону и с какой силой), т.е. равны ли Y(i|t=0) и Y(i|t=1) для любого i при фиксации других переменных (z_i), или, что еще лучше, определить разницу Y(i|t=1) — Y(i|t=0) для любого i=1..N. К сожалению, в реальной жизни один пользователь одновременно видит только одну версию сайта (один treatment), и мы не можем наблюдать все potential outcomes для него. Это называется fundamental problem of causal inference.
Если у нас есть юниты как с t=0, так и с t=1, то мы можем посчитать Y(i) для i c t=1 (для таргетной группы), затем Y(i) для i c t=0 (для контрольной группы), и вычесть. Это прекрасно работает, если все юниты одинаковые. Однако, в реальной жизни все пользователи разные, т.е. имею свой собственный вектор z_i.
Трюк, который нам помогает в А/В-тестах — вместо разности Y(i|t=1) — Y(i|t=0) для одного юнита, можно взять усреднение по всем:
ATE = E[Y(i|t=1)-Y(i|t=0)], где E — матожидание
Суть трюка проста — при достаточно больших выборках, финитных совместных распределениях z_i (считай, что это условие всегда выполнено в реальной жизни) и действительно рандомизированном разделении на группы в выборке с t=0 для каждого юнита найдется примерно похожий на него юнит из группы с t=1. В таком случае E[Y(i)] в первой группе будет равно E[Y(i)] во второй, как если бы обе выборки был под одной группой. Поэтому одно из основных предположений А/В-тестов — это all-else-equal сравнение, т.е. тестовые группы отличаются только фактором treatment’а (Ceteris paribus).
Этим мы пользуемся в А/В-тестах, когда фактически вместо ATE считаем его несмещённую оценку:
E[Y(t = 1)|t = 1] — E[Y(t = 0)|t = 0] ,
где E[Y(t =..)|t = 1] — средний potential outcome в таргетной группе , а E[Y(t =..)|t = 0] — в контрольной, независимо от того какой treatment effect мы тут применяем к каждой группе. Например: E[Y(t =0)|t = 1] — контрфактичесий (ненаблюдаемый) исход, что было бы если мы к таргентной группе применили treaetment контрольной.
Еще раз — для этого мы пользуемся тем, что treatment assignment и potential outcomes независимы (мы обсудим независимость ниже), а значит выполняется:
E [Yi (t=1)|ti = 1] = E [Yi (t=1)|ti = 0]
E [Yi (t=0)|ti = 1] = E [Yi (t=0)|ti = 0],
поэтому:
E[Yi(t=1)−Yi(t=0)]=E[Yi(t=1)]−E[Yi(t=0)]=E[Yi|ti=1]−E[Yi|ti=0]
Если мы внимательно посмотрим на формулу, то заметим еще один факт — наш потенциальный исход зависит только от treatment’а данного юнита, и вектор его параметров (константа для юнита), и никак не зависит от treatment’а других юнитов. Это предположение называется Stable unit treatment value assumption (SUTVA), и оно не выполняется в случае, если наши юниты зависимы (сетевой эффект, spillover). Также оно не выполняется если у нас есть несколько версии одного treatment — например, на часть пользователей мы выкатили фичу и отправили рассылку, на другую часть — только фичу. Еще одним предположением А/В, которое может нарушиться, является consistency.
Для бизнеса, однако, более важной является величина Average treatment effect on the treated (ATT):
ATT = E[Y(T = 1)|T = 1] — E[Y(T = 0)|T = 1] ,
определяющая разницу в таргетной группе между тем, какой потенциальный исход мы имеем (после применения маркетинговой акции или запуска новой фичи), и тем, каким он был бы в случае отсутствия treatment’а. По сути, эта величина определяет ATE на уровне тергетной группы, в то время как в классических А/В мы пытаемся оценить ATE на уровне всей популяции. Поскольку второй член в разнице мы не можем измерить, нельзя утверждать что A/B-тест рассчитывает ATT, в то время как некоторые из методов ниже именно этим и занимаются.
Также часто в бизнесе какая-то фича хорошо работает для одного сегмента клиентов, но плохо (или вообще негативно) для другого. Это называется гетерогенным эффектом (heterogeneous treatment effect). В таком случае более полезным является измерение Conditional average treatment effect (CATE), т.е. ATE на уровне определенного сегмента (subgroup):
CATE = E[Y(T = 1)|X = x] — E[Y(T = 0)|X = x]
Конечно, самой полезной величиной является определение эффекта на уровне конкретного пользователя (Individual treatment effect, ITE). В таком случае, мы можем показывать фичу только тем пользователям, на кого она повлияет заведомо положительно. Однако, как мы уже обсудили выше, это нельзя сделать в А/В, если только юниты не являются котами Шрёдингера. В третьей статье серии мы обсудим методы для оценки HTE/CATE/ITE.
Controlling for covariates в А/В-тесте
Иногда, в А/В-тесте мы не можем быть уверены, что тестовые группы сбалансированы (equalized) по всем ковариатам (covariates, которые в случае разбалансировки называются blocking factors). Например, в контрольной группе больше женщин, а в таргетной — мужчин, при этом целевая метрика в среднем различна между мужчинами и женщинами. В таком случае нарушается internal validity, т.е. степень уверенности, что различия между группами определяются именно фактором treatment’а, а не другими ковариатами. В литературе данная проблема встречается под названиями covariate shift и selection bias.

Пример (из неплохого введения и сборника методов) показан на картинке слева. Лекарство А более склонны принимать молодые люди, лекарство В наоборот. И хотя в каждом сегменте (Young и Older) лекарство А проигрывает, общий эффект противоположен (парадокс Симпсона).
Очевидным решением является учёт разницы в ковариатах при рассчете эффекта. Для этого нам необходимо контролировать ковариаты. Чтобы понять данную механику и вывести формулу, давай взглянем на А/В-тест с другой стороны:
Yi = Yi(0) + [Yi(1) − Yi(0)] · Ti
, т.е. потенциальный исход — линейная модель (y=β0+β1*x), где нулевой коэффициент (intercept) — исход юнита в контроле, а первый (slope) — индивидуальный эффект от воздействия. Единственное — в данной модели эффект константен, хотя почти всегда в реальной жизни он гетерогенен.
Теперь добавим и вычтем E[Yi (0)]:
Yi=E[Yi (0)] + [Yi(1)−Yi(0)]*Ti + [Yi(0)−E[Yi(0)]]
, и если мы усредним это уравнение, то получим модель y=β0+β1*x+β2*ui + e, где β1— и есть ATE. Член [Yi(0)−E[Yi(0)]] обозначим как ui в дальнейшем. Последний член e— это случайная ошибка, которая на самом деле является результатом неучтенных факторов.
Если мы обучим модель линейной регрессии, или просто сделаем корреляционный тест, мы получим ровно такой же p-value, как в t-тесте.
На самом деле, все стандартные статистические тесты являются линейными моделями в случае нормальных данных, подробнее читай тут https://lindeloev.github.io/tests-as-linear/.
Так вот, в случае разбалансировки таргетной и контрольной групп по какой-либо переменной (скажем мужской/женский пол), член ui в уравнении не будет равен нулю внутри каждой из групп, т.е. не выполнено условие E[ui|ti]=0. Однако, если внутри сегментов (только мужской и только женский пол) данное условие выполнено, т.е. E[ui|ti,Wi]=0 (здесь в качестве Wi обозначен пол юнита), то можно добавить Wi в уравнение, и оно станет валидным. Это называется Conditional Mean Independence, и мы еще обязательно к нему вернемся.
Yi = β0 + β1Xi + β2Wi +β3 ui + e
Решая такую регрессию, мы опять получим оценку ATE = β1, на этот раз несмещенную. Bingo 😊! Аналогично тому, что регрессия с одним параметром эквивалентна корреляционному тесту, контролирующая регрессия эквивалентна тесту частной корреляции.
Надеюсь, читателям данного блога не нужно объяснять, как строить линейную регрессию, но чтобы статья была self-contained, приложил код на python с использованием sklearn.
Добавляя таким образом несбалансированные ковариаты (баланс можно проверять обычными стат-тестами), мы будем получать все более точную оценку эффекта, и что более важно — уменьшать дисперсию (сужать доверительный интервал, повышая Коэффициент детерминации регрессии), а значит повышать мощность. Кстати, если в качестве ковариата взять целевую метрику за предыдущий период, то получим вездесущий CUPED, о котором сейчас слышно из каждого утюга. Важный момент — нельзя добавлять в ковариаты переменные, которые относятся к post-treatment периоду, ниже мы узнаем почему.
Напоследок — целевая метрика не всегда распределена нормально. А это — одно из требований для построения дов-интервалов и расчета стат-значисмости коэффициентов линейной регрессии (хотя это и необязательно для несмещенности оценок коэффициентов и минимизации RMSE, подробнее читай в последнем разделе другой моей статьи). Например денежные метрики (допустим, ARPU) часто распределены с сильной скошенностью вправо. В таком случае, вместо линейной регрессии, можно обучать негативно-биноминальную, а в случае, когда целевая метрика имеет много нулей — zero-inflated negative binomial регрессию. Подобные методы используются в данной статье. В случае биноминальной метрики (конверсии) можно использовать логистическую регрессию. Данный подход называется Generalized linear model, и его подробно разбирали Karpov.Cources.
Controlling for covariates в observational studies
Когда мы проводим квази- или натуральный эксперимент (quasi- and natural experiments), т.е. разделяем выборки не рандомом, а по какому-либо признаку, например гео (так любит делать Netflix), наши юниты в одной группе в среднем не равны юнитам в другой группе (иначе почему они оказались в разных группах??), а значит при сравнении мы будем получать систематическую ошибку отбора. Подобно тому, как мы контролировали ковариаты в А/В-тесте, мы можем делать это (adjust confounders) в не-рандомизированных экспериментах, а также в обсервационных исследованиях.
К сожалению, это наивный метод, который можно использовать только при определенных условиях. Дело в том, что на выбор интервенции (threatment’а) может влиять переменная, которая также влияет на outcome (целевую метрику). Такая переменная называется confounder. В подобных кейсах наблюдается “mixing of effects”, т.е. мы не можем напрямую отделить влияние интервенции от влияния конфаундера. Так объясняются все известные примеры ложных корреляций, например взаимное увеличение количеств потребляемого мороженного и утоплеников объясняется конфаундером — временем года.

Первый раз я увидел подобные кейсы в курсе статистики от Яндекса, в котором разбирался абсурдный на первый взгляд пример. В исследовании построили график зависимости уровня холестерина от уровня физической активности. Получается, что занятия спортом не делают человека здоровее, а ровно наоборот.

К счастью, все встает на свои места, если учитывать переменную-конфаундер. В данном случае это был возраст участников исследования. Слева можно видеть тот же график, на котором цветом выделена возрастная группа (когорта). Внутри каждой когорты зависимость уровня холестерина от физической активности принимает правильный, убывающий вид.
Так когда же конфаундеры можно использовать в контролирующей регрессии, а когда нельзя???
Confounders
Казалось бы, контроль за ковариатами приводит нас к честному подсчету эффекта, и этим методом можно с большой точностью заменить А/В-эксперименты. Но жизнь куда более сложная, и мы сталкиваемся с двумя фундаментальными предположениями этого метода, которые нарушаются в большинстве случаев.
- Ignorability (Unconfoundedness)
Чтобы добавить в модель конфаундер (не знаю как лучше перевести это на русский язык), про него нужно знать и его нужно измерять. Ситуация, в которой все необходимые мешающие факторы (вольный перевод слова confounder) содержатся в датасете, называется unconfoundedness (на самом деле это означает условную независимость выбора treatment’a и outcome’a). К сожалению, в реальной жизни такие ситуации — редкость. Если мы не наблюдаем какой-либо важный конфаундер, он добавляется в слагаемое ошибки в регрессии, которая в этот момент перестает быть случайной, а значит нарушаются предположения регрессии и она становится невалидной.
2. Неправильный граф
В упомянутом выше курсе от Яндекса есть иллюстрации двух конфигураций конфаундеров и зависимых/независимых переменных.

В первой — конфаундер “Возраст” влияет как на зависимую переменную “Холестерин”, так и на независимую “Упражнения”. Данная фигурация называется вилка, и модель регрессии здесь дает правильную оценку эффекта.

Вторая конфигурация называется коллайдрер, в ней уже сам конфаундер “Поступление” зависит как от независимой переменной “Средний балл”, так и от зависимой “Результаты интервью”. К сожалению, в данной конфигурации нельзя применять контролирующую регрессию (controlled regression on observational data). Именно поэтому в контролирующую регрессию нельзя добавлять в ковариаты из post-treatment периода.
Итого, про неправильный граф можно сделать следующие выводы:
- Добавление бОльшего кол-ва переменных в модель не всегда улучшает ее качество, а иногда приводит к противоположным оценкам эффекта.
- Имея на руках датасет, нельзя просто запустить “машинку” и получить результат (p-value кстати создавался именно для этих целей). Нужно иметь достаточно знаний о доменной области, позволяющих построить граф (об этом мы поговорим во второй статье).
- Иногда конфаундеры могут сложным образом взаимодействовать между собой, т.е. хотя E[ui|ti,Wi] != 0, но может быть что E[ui|ti,Wi_1, Wi_2, …, Wi_n] = 0. В таком случае линейная модель не сможет контролировать ковариаты и потребуются более сложные модели.
Matching Methods
Важным понятием, которое нужно осознать — является Conditional Independence. Как мы теперь знаем, один из главных столпов А/В-тестов — рандомизированное назначение интервенции (treatment’а), т.е. по определению из теорвера:
P(Y,t) = P(Y)*P(t)
В случае обсервационных исследований это не всегда так, поскольку присутствуют конфаундеры, через которых есть связь между назначением интервенции и outcome’ом🙈 🙉 🙊.
Однако, если зафиксировать значение конфаундера (обозначим вектор всех конфаундеров Z), то написанное выше уравнение начнет выполняться. Это и называется Условной Независимостью:
P(Y,t|Z) = P(Y|Z)*P(t|Z)
Человеческим языком это расшифровывается так — внутри одного сегмента (определяемого фиксированными значениями всех конфаундеров) можно сравнивать target с control’ом и при этом получать несмещённую оценку ATE (а точнее CATE ❗️), поскольку мы считаем что внутри этого сегмента юниты разбиты на группы как бы случайно (“as-if random”). Методы, использующие это, называются Conditioning-based.

Не считая обычную стратификацию, первым классом методов будут matching methods, хорошее изображения для которых можно найти на данном вебинаре от команды из Microsoft. На картинке изображены 2 группы людей — таргет, регулярно ездящий на велосипеде и обратный ему контроль. Задача — сравнить влияние поездок на велосипеде на уровень здоровья.

На следующем рисунке изображен механизм matching-метода — каждому юниту из таргета подбирается идентичный из контрола. Далее внутри каждой пары считается эффект, который затем можно усреднить для получения ATE (точнее ATT). Также отдельно дано пояснение — точного совпадения может не быть, но выбирается метрика “близости” (например расстояние Махаланобиса) и некий порог для нее. Юниты, расстояние между которыми меньше порога, считаются сматченными. Пример кода для данного метода мы рассмотрим в следующем разделе.
Данный метод обладает 2 недостатками, явно обозначенными на изображении. Во-первых — variance (дисперсия): большая часть юнитов может оказаться несматченной, а значит выборка будет небольшой. Во-вторых — bias (смещение): если увеличим кол-во матчей, подняв порог, то начнем сравнивать недостаточно идентичных юнитов. Получаем известный в ml-среде bias-variance tradeoff. Очевидно, что если target-выборка мала (скажем, натуральный эксперимент по оценке влияние непопулярной фичи), то большим будет как и bias, так и variance.
Matching — это не один метод, а целый класс, подробнее про них можно прочитать в ревью Matching Methods for Causal Inference: A Review and a Look Forward или в статье. Также данный метод можно встретить под названием Cohort Study (в статье написаны правильные вещи — не стоит путать cohort study с когортным анализом). Кстати, матчинг можно совмещать с контролирующей регрессией, в таком случае дисперсия результата будет гораздо меньше.
Стоит отметить, что данный класс методов также подвержен проблеме unconfoundedness’а, т.е. для его использования необходимо знать все значимые конфаундеры.
Propensity Score
Что же делать, если ковариаты имеют слишком большое количество значений или континуальны (имеют неограниченное число значений)? И как обойти проблему ненаблюдаемых ковариатов?
Можно сравнивать дистанцию не между ковариатами, а между некой функцией от них (в случае выполнения ignorability относительно этой функции, она называется balancing score).

Одной из таких функций может быть т.н. propensity score (PS). Это вероятность получить treatment=1, которую можно оценить/предсказать с помощью ml-моделей. Если взять в формуле logit от PS, то получим линейную метрики дистанции. Propensity Score Matching — один из самых старых методов, представлен в 1983г. Рассчитывать скор можно любыми методами, машинное обучение, например, лучше справляется с ненаблюдаемыми фичами, чем простой матчинг. Обычно используется логистическая регрессия. Модель не обязана быть очень точной, наоборот — при очень точной модели у нас не будет матчей.

Далее для каждого юнита из таргетной группы подбирается наиболее близкий по PS юнит из контроля (т.н. Greedy One-to-one Matching) и считается эффект между ними (Rubin в своей работе доказал, что ковариаты и treatment условно-независимы относительно PS). Есть несколько альтернативных версий метода — каждому юниту из таргета может соответствовать несколько юнитов из контроля, поэтому матчинг можно делать с возвращением и без (bias-variance trade-off). Также мы можем разбить весь диапозон PS на бины, и сравнивать между собой уже целые бины (в каждом бине считаем ATE и затем берем их взвешенную сумму). Такой подход называется стратификацией (Propensity Score Stratification) и изображен на рисунке слева.
Аналогично регрессии, для рассчета скора нельзя использовать post-treatment переменные, иначе получим ошибку под названием overmatching. Стоит сказать, что данный метод не в полной мере решает проблему ненаблюдаемых переменных, а в некоторых кейсах даже увеличивает bias (в отличии от других методов матчинга). Также метод PS, как и другие матчинг-методы, требует выполнения предположения positivity (совместное выполнение ignorability и positivity называется Strong Ignorability или Strongly Ignorable Treatment Assignment), означающего, что у каждого юнита есть шанс оказаться как в контрольной, так и в таргетной группе, т.е. PS должен лежать в открытом интервале 0<PS<1 и не попадать на его границы (эффект на границах называется Local Average Treatment Effect, LATE).
Пришло время пописать код ✍️. Воспользуемся python-пакетом от Uber под названием CausalML (прочитать про него можно тут). Этот пакет мне нравится тем (помимо того, что я просто люблю Uber), что он простой и небольшой (как по размеру, так и по функциям), легко устанавливается и имеет небольшое кол-во зависимостей. Также он вписывается в API других пакетов, о которых поговорим ниже. Предположим, что у нас есть пандосовский дата-фрейм, содержащий в своих колонках интересующую нас метрику, группу/метку (контроль или таргет), а также все необходимые ковариты. Тогда код слева натренирует модель, предсказывающую PS, cматчит по нему выборки и оставит только сматченную часть датафрема, по которой уже можно посчитать ATE. Помимо Nearest Neighbors есть также алгоритмы матчинга Caliper, Stratification, Kernels.
Кстати, метод PSM можно расширить и в случае сетевого эффекта (нарушение SUTVA), читай об этом тут и тут.
Inverse probability weighting (IPW): Как в обычном матчинге, так и в PS-стратификации на один сегмент может попасться не один юнит, а целый набор. При этом распределение кол-во участников в наборе между контролем и таргетом может несовпадать. В таком случае генерится “псевдо-популяция”, в которой подобные распределения совпадают (т.е. для одного уровня PS кол-во мужчин/женщин начинает совпадать в контроле и таргете). Данный метод именуют Inverse Probability Weighting (IPW), или Inverse Propensity Weighting, или Inverse Probability of Treatment Weighting (IPTW). Фактически, данный метод балансирует распределение какого-либо ковариата между группами.

Суть метода представлена слева (картинка из роскошной серии статей от Мелкомягких). Юниты из таргетной группы получают вес w(x) = 1/ps(x), а контрольная группа — w(x) = 1/(1-ps(x)). Оценивается эффект с помощью с помощью данной формулы (взято из хорошего овервью методов):

Существует несколько схем подобного перевзвешивания — например, на границах (PS близких к 0 или 1) высока дисперсия, поэтому данной паре/страте стоит давать меньший вес. Кстати, IPW можно совмещать с регрессией 2 разными способами — применять регрессию внутри каждой страты или использовать PS как один из ковариатов в регрессии ; подробнее можно прочитать тут, тут и тут.
Пришло время покодить и познакомиться с еще одним пакетом — DoWhy от Microsoft. Отличительная особенность в том, что в нем помимо методов для оценки эффекта основной упор делается на создание графа зависимостей и проверку предположений для каждого метода, и это мы разберем во второй части статьи. Что важно знать сейчас про этот пакет: во-первых, в нем содержится большинство методов, во-вторых — это пакет можно использовать как обертку над CausalML (который мы разобрали выше) и EconML (который мы разберем ниже), так что все недостающие методы можно брать из них. В общем, это универсальный интрумент, хотя и немного громоздкий. Кратко код для IPW можно написать так, как показано слева. Название метода propensity_score_weighting можно заменить на propensity_score_stratification/propensity_score_matching чтобы получить методы, обсужденные выше.
Подробнее про методы, связанные с Propensity Score можно прочитать тут и тут.
Doubly-robust
Данный метод можно встретить под названиями Doubly Robust Estimation (DRE), Doubly robust learning (DR) и Augmented IPW (AIPW). Важно не путать этот метод с Double-ML (тоже алгоритм примерно для того же), о котором еще поговорим ниже.
Мы рассмотрели выше 2 модели — регрессию и PS. Как и любые модели, они могут быть плохими, и для каждой задачи нужно выбирать лучшую. Но сейчас я покажу тебе лайфхак.

Можно комбинировать регрессию и PS, и комбинация будет корректна, когда корректна хотя бы одна из двух моделей (предположения хотя бы одной выполнены). Это и есть DR-метод, суть которого представлена на картинке слева (также понятнее может после просмотра слайда 30 тут). Доверительные интервалы можно построить также, как и для обычной регрессии. Кстати, вместо контролирующей регрессии и например логистической регрессии (для PS) можно использовать любые 2 ML-модели, которые будет предсказывать:
- Ковариаты и treatment -> Потенциальный исход (model_y)
- Ковариаты -> Какой treatment получит юнит (model_t)
К сожалению, данный метод будет давать очень смещенную оценку, если обе модели некорректны. Предположение Ignorability также требуется. Rubin показал, что если ковариат — монотонная функция от PS и матрицы ковариаций обоих групп верны (группы имеют одинаковые дисперсии), то регрессия убирает bias. В противном случае — метод может его сильно завысить.
Давай воспользуемся python-пакетом, который я уже упомянул — EconML. Этот пакет будет блистать в третьей части статьи, а пока воспользуемся им для реализации DRE.
Код представлен слева (взят из примера-ноутбука). Хорошей особенностью является то, что вместо представленных LassoCV (model_y) и DummyClassifier (model_t) можно использовать любые подходящие модели из sklearn.
Вместе с IPS, это метод часто используется в офлайн тестах, которые так популярны в последнее время и в англоязычном варианте именуются Offline Policy Evaluation.
Расширением данного метода является Targeted Maximum Likelihood Estimator (TMLE), который требует обучить еще 3ю модель. Не буду углубляться и отправлю к уже упомянутому обзору и оригинальной статье.
Instrumental variables (IV)
Все предыдущие методы использовали предположение ignorability, которое сложно проверить и которое часто не выполняется. Теперь рассмотрим методы, робастные к его невыполнению.

Мы рассматриваем кейсы, где назначение интервенции не рандомизировано и на наш treatment влияет конфаудер. Но что если мы сможем найти или сделать переменную, которая будет рандомизированной и при этом влиять только на treatment. Такая конфигурация показана на картинке слева (взято из курса). Видно, что конфаундер не влияет на инструментальную переменную.
Очевидный плюс метода — нам не обязательно наблюдать все конфаундеры (предположение ignorability). Важно только сохранять конфигурацию: инструмент влияет только на интервенцию (и только через нее влияет на outcome), и независим от конфаундеров (данное предположение называется exclusion restriction).
Приведу пример: допустим, мы хотим изучить влияние пользования фичей на деньги. Как мы уже знаем, напрямую сравнивать тех, кто пользуется, и тех, кто не пользуется, нельзя. Что мы можем сделать — рандомизированные рассылки о новой фиче, факт рассылки и будет нашей инструментальной переменной. Мы ожидаем, что попадание в группу с рассылкой будет коррелировать с использованием новой фичей. Часто такой “инструмент” называют encouragement.
Для оценки эффекта применяется two-stage регрессия (2-Stage Least Squares, 2SLS), где мы вначале строим 2 регрессии: treatment’а от инструмента (z->t) и outcome’а от инструмента (z->y).
В отличии от регрессии treatment->outcome, вторая регрессия (z->y) становится валидной поскольку слагаемое ошибки (сумма внешних факторов) уже на зависит от переменной регрессии.
Далее делим slope второй регрессии на slope первой: ATE = Cov(Y, Z) / Cov(T, Z).
Конечно, можно использовать вышеупомянутый код для регрессии (или statsmodels.api.OLS), и самому посчитать отношение. Но проще воспользоваться уже знакомыми нам пакетами. Мы использовали CausalML, DoWhy и EconML. Пора идти на второй круг и опять воспользоваться CausalML от Uber. Код на нём для рассчёта ATE приведен слева.
В отличие от нижеописанных методов, которые появились в последние года, статья по инструментальным переменным вышла почти 30 лет назад. Казалось бы, если есть такой простой и хорошо изученный метод, то зачем нужно что-то другое ❓. Дьявол, как всегда, кроется в деталях — в реальной жизни довольно сложно найти подходящий инструмент, поскольку почти всегда он будет также влиять непосредственно на outcome (direct-эффект), а не только через treatment. Если же предположения инструмента (независимость от наблюдаемых и ненаблюдаемых конфаундеров) не выполняются, данный метод даст сильно смещенную оценку эффекта. К сожалению, это метод также требует гомогенность (противоположность гетерогенности) хотя быть одного из двух эффектов: IV->treatment или IV->outcome.
У данного метода также есть расширения, например Double Machine Learning Instrumental Variables (DMLIV), или Doubly robust Instrumental Variables (DRIV), Deep IV или Intent To Treat DRIV. Данные методы можно найти в python-пакете EconML.
Time-series
Надо помнить, что все condition-based методы (регрессия — это тоже condition-метод с континуальной переменной) требуют соблюдения предположения SUTVA, что, очевидно, выполняется не всегда (нарушения SUTVA нивелируются также, как в А/В — изменением сущности тестирования и кластерный анализ).
Проблемой предыдущих методов может являться плохое покрытие данными всех возможных комбинаций конфаундеров.
Также condition-based методы страдают от проблемы, которая типична и в ML — Проклятие размерности, когда у нас очень много фич и мало матчей. Однако, решения данной проблемы также заимствуются из ML— снижение размерности, регуляризация, преобразование фич и обучение низко-размерных репрезентаций.
Еще одна проблема связана с возвращением к среднему — при as-if random назначении treatment’а мы сравниваем юниты из контроля и таргета, поскольку ожидаем, что они одинаковы. В реальности они могут быть разными, просто в данный момент времени пересекаются на граничных случаях — худшие из таргета матчатся с лучшими из контроля. Но, учитывая возвращение к среднему, в другой момент времени данные юниты могут оказаться несравнимыми.
Учитывая перечисленные недостатки condition-методов, нужно найти что-то более робастное. Заметим, что все упомянутые выше методы использовали только 1 точку во времени — уже после интервенции. Но в большинстве случаев у нас есть гораздо больше данных — как о pre-treatment, так и о post-treatment периоде. Т.е. мы обладаем time-series (панельными) данными, и можем сравнивать не только группы между собой в 1 временной точке, но и одну группу между разными периодами времени. На этом основаны низлежащие методы.
Regression Discontinuity Design (RDD)

Часто используется интересный дизайн квази-эксперимента, называемый Regression Discontinuity Design (RDD) — в нем назначение интервенции определяется по определенному порогу (cut-off). Анализ довольно простой — поскольку назначение treatment’a определяется скачком, то и outcome (значение точки на линии регрессии) изменится тоже скачком. Влияние конфаундеров здесь контролируется так — предполагается, что точки сразу до и после разрыва близки, а значит имеют одинаковые конфаундеры (похоже на натуральный эксперимент, где мы рандомно разделили облако точек рядом границей раздела). Есть достаточное кол-во литературы по анализу таких экспериментов, например от Принстона (раз, два) или mdrc.
Единственное требование для RDD — метрика должна быть выбрана так, чтобы она могла измениться мгновенно, без задержек. Вместо прямой можно моделировать линию с помощью других непрерывных (т.е. все же regression) функций, но вот статья которая говорит что полиномы высших степеней использовать не стоит. Поговаривают, что RDD это специфичный кейс IV (переменная, означающая перешел ли юнит порог или нет — инструментальная). Поэтому метод находится в модуле iv пакета DoWhy. Допустим, мы уже получили объект identified_estimand так, как показано выше в коде для IPW. В таком случае эффект методом RDD можно оценить так:
Diff-in-Diff (DiD)

Итак, мы можем использовать данные о разнице между контрольной и таргетной группой до эксперимента (квази- или натурального), тем самым учитывать влияние конфаундеров! Картинка, поясняющая метод, взята из статьи на медиум.
Суть метода в том, что мы используем 4 значения (2 пары) целевой метрики: контрольной и таргетной группы до интервенции ( C1 и T1), а также контрольной и таргетной группы после интервенции ( C2 и T2). В случае, если эффекта нет, разнится внутри этих пар должна быть одинаковой. Если же разница непостоянна, она аттрибутируется к измеряемому эффекту.

Сам метод довольно прост, и код для его рассчета настолько очевиден, что нет смысла его тут показывать. Cлева пример использования и рассчета от DS из Coursera (правый нижний угол дает ответ). DiD — аналог CUPED, но с коэффициентом для pre-experiment данных равным 1.
Предположение для DiD — параллельность прямых. Также он предполагает отсутствие spillovers (сетевого эффекта). Данный метод (как и все) имеет расширения. Например, можно попытаться контролировать конфаундеры. Показано, что в DiD будет ошибаться в случае HTE!
DiD (наличие контроля) и предыдущий метод RDD (наличие разрыва) можно объединить в один большой класс методов под названием Interrupted time series (ITS), к нему же можно отнести и следующий метод (synthetic control). В целом, DiD, RDD, ITS можно свести к регрессии, читай тут. Если хочется еще усложнить данный метод (ввести параметрику и априорные значения, исследовать несколько treatment’ов), можно воспользоваться Bayesian structural time series (BSTS), например так делает Booking.
Synthetic-control (SC)
Может возникнуть ситуация, что не будет достаточного количества матчей между контрольной и таргетной группами. Например, в самом начале пандемии прививки делали только возрастным пациентам, которых нельзя сравнивать с более молодой аудиторией. Хотя в таком случае у нас не окажется подходящего по значениям конфаундеров контроля, мы можем попытаться построить (например с помощью ML) “псевдо-популяцию” на основе контрольной группы, которую уже можно матчить с таргетной. Упомянутый DiD можно назвать самым простым методом SC, однако он не учитывает изменение конфаундеров во времени (предположение о параллельности). Лучше 1 раз нарисовать (спасибо Uber, что сделали это за меня), чем много раз объяснить:

Самый простой способ — собрать псевдо-юнит взвешенной сумой юнитов из контрольной группы так, чтобы на pre-treatment периоде его outcome был максимально близок к outcome таргетной группы. В отличии от DiD, мы не предполагаем, что все юниты в контроле имеют общий тренд с таргетной группой, а лишь находим тех, для кого это предположение верно.

Замечательная особенность данного подхода в том, что мы можем использовать множество временных периодов.

На рисунке слева (из этой статьи) показана линейная модель, на которой веса подбираются с помощью решения OLS. Как видно, мы можем их получить из среднего outcome таргетной группы на pre-treatment периоде (x1), затем использовать на post-treatment (x2). Тогда ответ модели Y(x2) и будет нашим синтетическим контролем. Это похоже на то, что как Avito подбирает контроль для региональных тестов, только вместо подвыборки из всего контроля с коэффициентом 1, данный метод использует полную контрольную группу с коэффициентами, найденными регрессией. Кажется что они должны сойтись (регионам-выбросам регрессия даст коэффициент 0), однако в случае коррелированных регионов (а такие точно есть) может возникнуть стандартная проблема и понадобится регуляризация. Кстати, интересно попробовать комбинировать 2 метода. Для экономии места код приводить не буду, возьми из статьи выше. Метод придумал A. Abadie, к сожалению, он прогает на R, потому нормальные пакеты только под него.
Интересная особенность SC, как и любого time-series метода — возможность изменять период тренировки по усмотрению экспериментатора (его знаний в доменной области). Ещё можно давать разные веса разным точкам, например, понижать значимость более ранних временных интервалов, благо sklearn почти любую стандартную модель умеет обучать с весами.
Важный нюанс SC (как и любого time-series метода) — нельзя использовать стандартную формулу для доверительного интервала для временных данных, ибо есть такая сложная штука как long-run variance (для других методов DoWhy рассчитывает дов. интервал с помощью бутстрап и еще чего-то непараметрического). Так чем же пользоваться, спросишь ты? Наш псевдо-соотечественник придумал вариацию t-теста для SC, но опять же это сложная штука и реализована пока только в R.
Continuous treatment, Double machine learning
Теперь давай представим, что наш treatment не бинарный, а дискретный или континуальный (ранг в поиске, процент скидки и тд). Конечно, можно использовать самый первый озвученный метод — регрессию, но она будет давать очень смещенные оценки эффекта в случае, если в реальности зависимости от ковариатов нелинейны (а обычно так и есть), или ковариатов очень много и их матрица ковариаций плохо обусловленна.

В таком случае нам поможет недавно представленный (всего 5 лет назад, тем же человеком что и двумя абзацами выше) метод DML. Он похож на DRE (в нем также перевзвешивание используется для остатков регрессии), но, в отличие от DRE, первая модель обучается только на ковариатах, а не на ковариатах+treatment.
Т.е. вначале мы обучаем 2 модели:
- Ковариаты -> Потенциальный исход (model_y)
- Ковариаты -> Какой treatment получит юнит (model_t)
Далее на остатках двух моделей тренируем регрессию, slope которой и будет эффектом. Обсудим теорию чтобы понять, почему это работает.
Рассмотрим простой пример — у нас есть регрессия y=β0+β1* t+β2*ui + e. Для оценки β1, мы можем воспользоваться теоремой Frisch–Waugh–Lovell, которая говорит о том, что можно построить регрессию y ~ ui, а остатки этой модели уже отрегрессировать на t (y ~ t). В таком случае эффекты двух моделей будут ортогональны (DML иногда называют Orthogonal ML), т.е. как бы вычтены друг из друга. Код и пример можно найти тут.
Если заменить регрессию в примере выше на сложные непараметрические модели, то получим DML. Данный метод можно найти в пакете EconML и в пакетах-близнецах для R (в статье помимо пакета также хорошо расписана теория) и Python от того же Черножукова.
Код для чистого EconML приведен в ноутбуке из документации. Но, как я уже говорил, можно использовать DoWhy как обертку надо EconML. Слева представлен именно такой вариант. Как видно, в данный метод нужно передать 2 модели из sklearn (насколько я знаю, можно использовать и другие библиотеки), которые будут соответствовать описанным выше.
Как ты уже догадался, поскольку DML находится в модуле backdoor (мы обсудим что это значит во второй статье), данный метод также подвержен проблеме unconfoundedness’а.
В целом, это сложный метод, который требует выполнения нескольких предположений (таких как гетероскедастичность ошибок) и хороших ML-моделей (смотри теорию тут). Если ты не понимаешь, что это значит и как это проверить, тебе не стоит использовать данный метод.
Кстати, для continuous treatment можно использовать и diff-in-diff.
На этом первая часть (самая легкая) заканчивается. Я уже анонсировал выход второй и третьей части, жди! Напоследок, краткий гайд, когда какой метод использовать (взят из статьи от Uber):
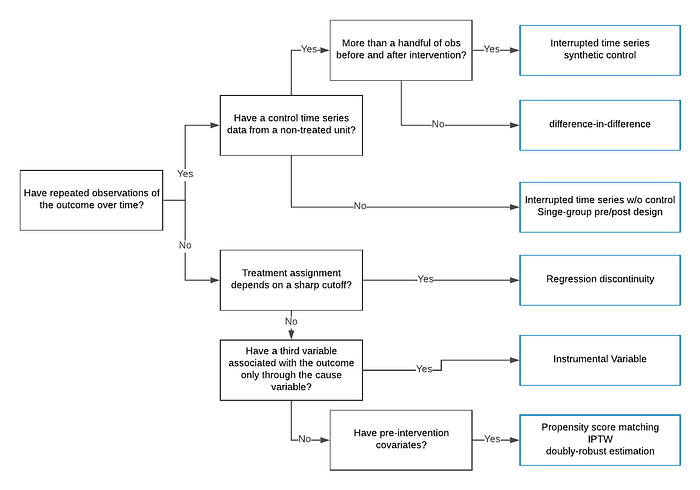
Кстати, лови хак для быстрой проверки на causation — если А следствие В, то B должно предшествовать А по времени (взял тут) ⏰. Еще один лайфхак — репо ноутбуков со всеми методами, а также книга с кодом.
Ну и до скорых встреч 😚 !!!
P.S.: Если тебе понравилась стать, в качестве благодарности можешь купить мне кофе на https://www.donationalerts.com/r/stats_data_ninja или https://buymeacoffee.com/koch.
